Math Fun

That’s where I am, too:

[tab]The fact that both numbers are between 2 and 99 means the product cannot be a prime number. The first thing Peter says, then, tells us the product is not a number that can only be divided by one or two other numbers than 1 and itself (for instance, 9 only by 3 and 8 only by 2 and 4). The second thing Sarah says tells us that she didn’t know the numbers yet when she said the first thing she said. The first thing she said, then, tells us the sum is a number that can be arrived at by multiple sets of two numbers (e.g., 8, by 2 and 6 and by 4 and 4). The second thing Peter says then tells us that the sums of the possible numbers of which he knows the product contain only one number for which that goes (for instance, if the product is 12 the sum can only be 7 or 8, and 8 is the only number of the two for which the aforesaid goes (the product 10 was already precluded by the first thing Peter said)). Now if the numbers are 2 and 6, Peter knows they are as soon as Sarah tells him she knows that he didn’t know the numbers (for then the sum must be 8 and not 7).[/tab]

Not the answer, but might reveal more information that people want to know:
[tab]I got it with heavy reliance upon Excel tables, formulas, and conditional formatting to simplify the brute force parts. The brute force seems to be inescapable, as the problem statement at the Post suggests.[/tab]
The answer and how I got there:
[tab]Peter’s statement that he doesn’t know doesn’t tell us much. There are actually a lot of numbers that are ruled out immediately:

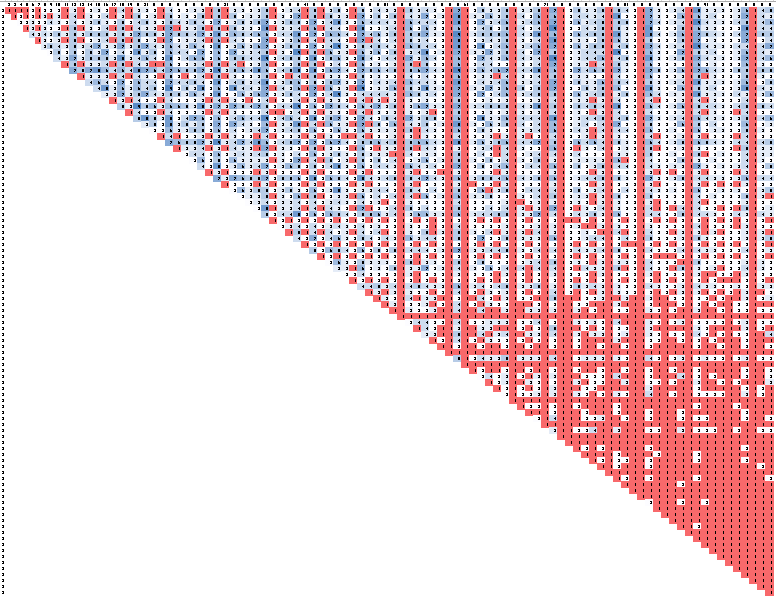
This is a table of all the possible products (zoomed way out, the big picture is what’s important here). Along the top and left are numbers 2-99, and the product of any two numbers is at the intersection of the respective row/column(2x2 is in the upper left, 99x99 is in the lower right). For simplicity, I only filled in the upper half of the table, since the lower half is identical. Cells highlighted in red appear more than once; those in white are unique. From Peter’s statement, we know that it’s none of the unique values (otherwise he would know immediately), but that doesn’t get us very far.

Sarah’s statement, “I knew you didn’t know” tells us that whatever sum she has, every product of every pair of integers that sums to that is non-unique. If there were two numbers that added to the number she knows, and multiplied to a unique product, then she wouldn’t know whether or not Peter knew.

This table shows the number of times each product appears in the entire set. Red cells appear once, white cells twice, and the bluer the more the appear from there. This chart wasn’t necessary, it was the result of what turned out to be a dead end, but it makes it a little easier to see some patterns and it’s just s’damn pretty, I didn’t want it to go to waste.

For any sum, there will be a diagonal line sloping up and right that has the same sum (because, e.g., 6+5 = 7+4 = 8+3 = 9+2 = 11). So in this chart, I was looking for the sloping lines that don’t contain unique values, i.e. that had no reds. This immediately eliminates everthing to the right of the solid red column around the middle of the chart (53xY): every diagonal line that extends beyond that column will have at least 1 unique product, and we need diagonal lines that have no unique products. There are relatively few lines, and we can take the list of sums corresponding to those lines: 11,17,23,27,35,37,41,47,53. We know the sum is one of those numbers.

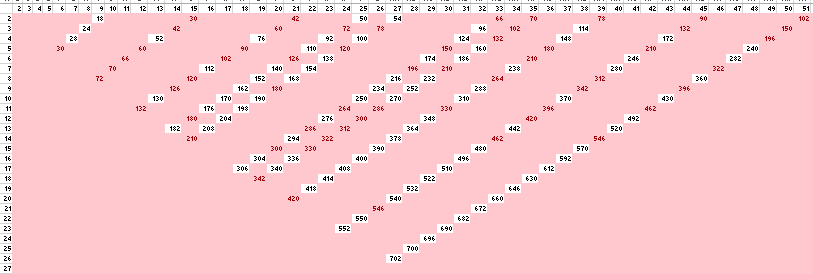
Peter’s next answer tells us that, among the pairs that sum to 11,17,23,27,35,37,41,47, or 53, his number must be unique: if it appeared in two of the diagonally sloping lines, he wouldn’t know from Sarah’s statement which line it was in, i.e. what the sum of the numbers is. So I made this chart:

This shows only the products that correspond to the available sums, and it’s highlighted to show duplicates (pink if a number appears more than once, white if not). Peter’s number is one of the numbers in white.

Finally, we look at Sarah’s last statement. Peter knows because his product is one of the values in white on the previous chart, that is, there is only one combination of numbers that falls along the diagonally sloping lines that has a product equal to the one he knows. This is enough to tell Sarah what number it is only if it is the only value in white with the sum she knows. And if we look along the diagonal lines, we see that 52, at the intersection of 4 and 13, is the only white number in its line (the line of numbers that sum to 17), and that no other line has such a number.

And so, because Sarah knows the answer, we know the answer. QED[/tab]

Well, okay. I couldn’t see that very last step of yours, Carleas (and still digesting it). Otherwise I had the exact same process (although my colors were better ).

The very first thing that threw me off was that I was concerned about the order of the numbers proposed, later deciding that they weren’t bothering with which order, but merely which two numbers.

[tab]I had that thought too, and I considered (and fortunately rejected) focusing on the square numbers (since if we actually had to say which number is A and which is B, we could only do that if they were the same number), especially since the problem statement made explicit that they could be the same number.

I haven’t spent too much time on it, but I don’t think the problem is solvable with that assumption.[/tab]

[tab]It just didn’t occur to me that she could choose which number he had chosen simply by the sum that she already had, thus I was checking out every possible combination of potential confusion.

But you got it right. She could chose which that he had chosen because she knew the necessary sum … simple enough.
Congrats.[/tab]

Prime numbers between 3 and 99:

5      7     11     13     17     19     23     29 
 31     37     41     43     47     53     59     61     67     71 
 73     79     83     89     97

Why can’t they be prime?

Eh?

Is that in the problem?

No matter what the solution to this one, the distintion between a and b is mute. Once again - badly worded, as not matter how cleverly you come up with some two numbers that work, without a subtraction in the mix, you can’t determine which of the numbers is a and which is b.

Lev, was the red print yours? …that you don’t get that part?

If so;
[tab]Einstein knew the month.
Bernard knew the day.

If Bernard could not deduce possibly the month from knowing the day, the month could not be May or June.
If it was even possible that perhaps Bernard could know the month after only hearing the day, that month would have to have a unique day mentioned. Because he could not possibly know the month regardless of whatever day he heard, the month could not have been May or June.[/tab]

They can’t be prime because prime numbers can only be a product of 1, which is disallowed.

Carleas, I think what’s commendable about your solution is not the Excell sheets but your grasping things like [tab]Sarah’s statement, “I knew you didn’t know” tells us that whatever sum she has, every product of every pair of integers that sums to that is non-unique.[/tab]

[tab]If the question was “What is a and what is b?”, then Peter would have known the numbers immediately.[/tab]

[tab]A prime number is a number that can only be divided into integers by 1 and by itself. But that would mean at least one of the two numbers was 1, which is impossible, as both numbers lie between 2 and 99.[/tab]

I think that there might be a way to narrow the pool of numbers to a much smaller amount right from the start. I’m brushing up on my number theory, haven’t played with any of this in over 10 years

[tab]What I am trying to remember is the particularities of adding and multiplying prime numbers. Correct me if I am wrong, but I think that all non-unique products need to have A as a prime number, and B as a product of two prime numbers. Then, you can break down the multiplication to (A1*A2)*B, where all 3 are prime. Your spreadsheet would be tridimensional, but it would look only at prime numbers, so the possible results would be a much smaller amount of numbers.

Hm… Actually, I think that non-unique products would be the product of at least three prime numbers, but not necessarily 3. Still, might be a good place to start.

Unless I’m completely wrong. Maybe one of you math dorks can confirm this and save me the trouble of actually studying the problem [/tab]

Numbers Theory was the only math course I didn’t take many years ago (I didn’t know that I would end up in philosophy) and just a practical note;
You don’t want to be preferring more than 2 dimensional arrays in Excel, unless they are very small or you are merely using the VBA.

[tab]I thought this one was interesting because it involved 10 prime numbers except for only one of them.
Why only prime except for one?!?![/tab]

[tab]No wait, that’s only if he knew that it was possible to know what was a and what was b. But there’s no reason to think that Peter and Sarah knew the question posed to us, let alone before they started talking. Anyway, the problem cannot be solvable with that question, as the numbers can only be 4 and 13; nor is it possible, from the information given, to tell which is which.[/tab]

More than the Sum of Its Parts

Just think about it.

Count them.

Both very clever illusions, especially the second.

First:
[tab]The hypotenuse is not quite strait. The visual effect is subtle, but you can calculate the slopes easily: for the red triangle it’s 3/8, and for the green triangle it’s 2/5. The result is the combined hypotenuse bends slightly in for the first triangle, and slightly out for the second, and that bend accounts for a 1x1 unit difference.

I’m sure there’s a more mathematically precise way to put this, but this satisfies me that the laws of mathematics aren’t being locally suspended [/tab]

Second:
[tab]This is a very impressive illusion. Even once I saw it, it’s still hard to believe that someone could come up with it and execute it.

The trick is that, rather than one person being completely removed between one version and the next, different parts of different people are removed by combining and splitting. So e.g., one person’s bottom half of a foot becomes another’s whole foot. It’s hard to identify who’s losing or creating what because it seems like everyone gives a little bit and the result is another full person.

Totally fascinating, thanks for this James.[/tab]

Right on both counts.

It is interesting to me how inventive some humans can be while still so devastatingly blinded.

Well done, James. =D>

This thread is obviously interesting.